Answer:
i. Point of estimate:

ii. Margin of error:

iii. The 90% confidence interval
Replacing in the confidence interval formula we got
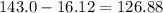
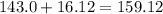
The 90% confidence interval is 126.88 to 159.12
Explanation:
Information given
 represent the sample mean for the variable of interest
represent the sample mean for the variable of interest
 population mean
population mean
s=56.7 represent the sample standard deviation
n=50 represent the sample size
Confidence interval
The confidence interval for the true mean when we don't know the deviation is given by the following formula:
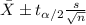 (1)
(1)
In order to calculate the critical value for the confidence interval
 we need to find the degrees of freedom, with this formula:
we need to find the degrees of freedom, with this formula:
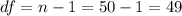
The Confidence level provided is 0.90 or 90%, the value for the significance is
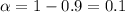 and
and
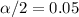 , and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.05,49)".And we see that
, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.05,49)".And we see that
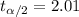
i. Point of estimate:

ii. Margin of error:

iii. The 90% confidence interval
Replacing in the confidence interval formula we got
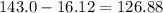
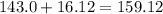
The 90% confidence interval is 126.88 to 159.12