Question

A company has 2 machines that manufacture widgets. An older machine manufactures 25% defective widgets, while the new machine manufactures only 9% defective widgets. In addition, the new machine manufactures 70% of widgets while the older machine manufactures 30% widgets. Given a randomly chosen widget was tested and found to be non defective, what is the probability it was manufactured by the new machine? Round the answer to 4 decimal places.

Answer 1

73.90%

Explanation:

Let Event D=Defective, D' = Non Defective

Let Event N=New Machine, N' = Old Machine

From the given information:

`P(D|N')=0.25\\P(D|N)=0.09\\P(N)=0.7\\P(N')=0.3`

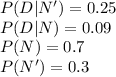
We are required to calculate the probability that a widget was manufactured by the new machine given that it is non defective.

i.e.
`P(N|D')`

`P(D'|N')=1-P(D|N')=1-0.25=0.75\\P(D'|N)=1-P(D|N)=1-0.09=0.91`

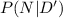
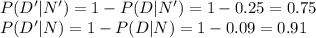
Using Baye's Law of conditional Probability

`P(N|D')=(P(D'|N)P(N))/(P(D'|N)P(N)+P(D'|N')P(N')) \\=(0.91*0.7)/(0.91*0.7+0.75*0.3)\\ =0.73897\\\approx 0.7390`

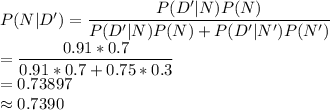
Therefore given that a selected widget is non-defective, the probability that it was manufactured by the new machine is 73.9%.