Question

Find the probability that a randomly selected person

from this sample liked recreational reading OR
disliked recreational reading.
P (likes recreational OR disliked recreational) =

Answer 1

1

Explanation:

right on khan

Answer 2

The probability that a randomly selected person from this sample liked recreational reading or disliked recreational reading is 1.

Explanation:

The probability of an event E is the ratio of the favorable number of outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

Mutually exclusive events are those events which cannot occur together. They are also known as disjoint events.

If events A and B are mutually exclusive then:

`P(A\cap B)=0`

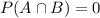
The data provided is:

Opinion Like academic Dislike academic Total

reading reading

Liked recreational 136 40 176

reading

Disliked recreational 16 8 24

reading

Total 152 48 200

Denote the events as follows:

X = a person liked recreational reading.

Y = a person disliked recreational reading.

Compute the probability that a randomly selected person from this sample liked recreational reading or disliked recreational reading as follows:

`P(X\cup Y)=P(X)+P(Y)-P(X\cap Y)`

`=(176)/(200)+(24)/(200)-0\\\\=(176+24)/(200)\\\\=1`

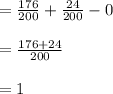
Thus, the probability that a randomly selected person from this sample liked recreational reading or disliked recreational reading is 1.