Question

A 0.16-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 140 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is x = -1.2×10−2 m, find the acceleration of the block.

Answer 1

The magnitude of the acceleration is
`a = 10.5 m/s^2`

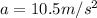
Step-by-step explanation:

From the question we are told that

The mass of the block is
`m = 0.16 \ kg`

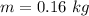
The spring constant is
`k = 140\ N/m`

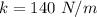
At first displacement is
`x = + 0.080 m`

At second displacement is
`x = -1.2 *10^(-2) \ m`

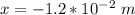
The acceleration at second displacement is mathematically represented as

`a = (k)/(m) * x`

`a = - (140)/(0.16) * 1.2 *10^(-2)`

`a = - 10.5 m/s^2`

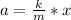
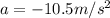
Therefore the magnitude of the acceleration is

`a = 10.5 m/s^2`

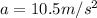
And the direction is in the negative x-axis