Question

vgUse technology to find the​ P-value for the hypothesis test described below. The claim is that for a smartphone​ carrier's data speeds at​ airports, the mean is mu μ equals = 17.00 17.00 Mbps. The sample size is n equals = 22 22 and the test statistic is t equals = negative 1.576 −1.576.

Answer 1

`t_(calc)= \pm 1.576`

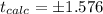
Now we need to find the p value , we need to take in count that we are conducting a bilateral test so then the p value can be calculated with this probability:

`p_v = 2*P(t_(21)<-1.576) =0.12997`

And we can find this p value with the following excel formula for example:

"=2*(T.DIST(-1.576,21,TRUE))"

Explanation:

For this case they want to conduct a test in order to check if the true mean for the smartphone carrier's data speeds is equal to 17 Mbps, so then the system of hypothesis are:

Null hypothesis:
`\mu = 17`

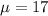
Alternative hypothesis:
`\mu \\eq 17`

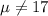
The statistic to check this hypothesis is:

`t= (\bar X -\mu)/((s)/(√(n)))`

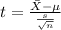
Since we don't know the true population deviation. We know that the sample size is equal to n =22, so then we can find the degrees of freedom given by this formula:

`df = n-1 = 22-1=21`

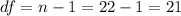
After replace in the statistic formula we have the statistic provided:

`t_(calc)= \pm 1.576`

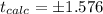
Now we need to find the p value , we need to take in count that we are conducting a bilateral test so then the p value can be calculated with this probability:

`p_v = 2*P(t_(21)<-1.576) =0.12997`

And we can find this p value with the following excel formula for example:

"=2*(T.DIST(-1.576,21,TRUE))"