Answer:
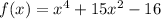
Explanation:
It is given that the leading coefficient of the polynomial is 1.
We need to find a polynomial function f of the least degree.
If c is a root of a polynomial then (x-c) is a factor of the polynomial.
The given zeros are -1, 1, -4i, 4i. So,
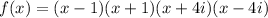

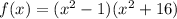
![[\because i^2=-1]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7zkfp9fycbczp657j2ujjh7ygl4k1wk7qx.png)

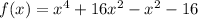
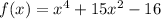
Therefore, the required polynomial is
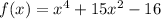 .
.