Question

The American Community Survey showed that residents of New York City have the longest travel times to get to work compared to residents of other cities in the United States. According to the latest statistics available, the average travel time to work for residents of New York City is 38.3 minutes. What is the probability it will take a resident of this city between 17.24 and 42.13 minutes to travel to work?

Answer 1

The probability for a person from the city is between 17.24 and 42.13 minutes to travel to work is 0.3046.

Explanation:

Answer 2

The probability it will take a resident of the city between 17.24 and 42.13 minutes to travel to work is 0.3046.

Explanation:

The random variable X can be defined as the travel times to get to work.

The expected travel time is, μ = 38.3 minutes.

The distribution of random variable X can be defined as the distribution of time interval between which a person reaches their work place at a constant average rate.

This implies that X follows an Exponential distribution with parameter,
`\lambda=(1)/(\mu)=(1)/(38.3)`.

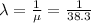The probability density function of X is:

`f_(X)(x)=\lambda e^(-\lambda x);\ x\geq 0`

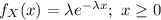
Compute the probability it will take a resident of the city between 17.24 and 42.13 minutes to travel to work as follows:

`P(17.24\leq X\leq 42.13)=\int\limits^(42.13)_(17.24){(1)/(38.3) e^(-x/38.3)}}\, dx`

`=(1)/(38.3)* \int\limits^(42.13)_(17.24){ e^(-x/38.3)}}\, dx`

`=(1)/(38.3)*| (e^(-x/38.3))/(-1/38.3)}|^(42.13)_(17.24)\\`

`=-e^(42.13/38.3)+e^(17.34/38.3)\\=-0.3329+0.6375\\=0.3046`

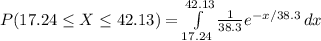
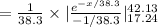
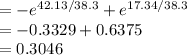
Thus, the probability it will take a resident of the city between 17.24 and 42.13 minutes to travel to work is 0.3046.