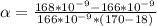Complete Question
A thin uniform film of refractive index 1.750 is placed on a sheet of glass with a refractive index 1.50. At room temperature ( 18.8 ∘C), this film is just thick enough for light with a wavelength 580.9 nm reflected off the top of the film to be canceled by light reflected from the top of the glass. After the glass is placed in an oven and slowly heated to 170 ∘C, you find that the film cancels reflected light with a wavelength 588.2 nm .
What is the coefficient of linear expansion of the film? (Ignore any changes in the refractive index of the film due to the temperature change.) Express your answer using two significant figures.
Answer:
the coefficient of linear expansion of the film is

Step-by-step explanation:
From the question we are told that
The refractive index of the film is
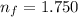
The refractive index of the glass is
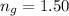
The wavelength of light reflected at 18°C is
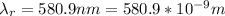
The wavelength of light reflected at 170°C is
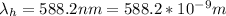
For destructive interference the condition is
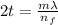
Where m is the order of interference
t is the thickness
For the smallest thickness is when m= 1 and this is represented as
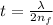
At 18°C the thickness would be
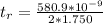
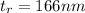 \
\
At 170° the thickness is
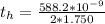
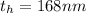
The coefficient of linear expansion f the film is mathematically represented as
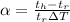
Substituting value