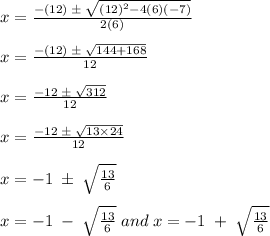Question

What are the zeros of the quadratic function f(x)=6x^2+12x-7

Answer 1

Use the quadratic formula

[-12 +/- square root (12^2- (4)(6)(-7))]/2(6)

[-12 +/- square root (312)]/12

-1+(1/6) square root (78)

and

-1-(1/6) square root (78)

Answer 2

By using the quadratic formula, the zeros of the quadratic equation are: A.
`x = -1 \;- \;\sqrt{(13)/(6) } \;and\;x = -1 \;+ \;\sqrt{(13)/(6) }`

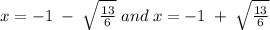
In Mathematics and Geometry, a quadratic equation can be defined as a mathematical expression that can be used to define and represent the relationship that exists between two or more variable on a graph with a maximum exponent of two (2).

In Mathematics, the standard form of a quadratic equation is represented by the following equation;

`ax^2 + bx + c = 0`

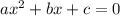
Mathematically, the quadratic formula is represented by this mathematical equation:

`x = (-b\; \pm \;√(b^2 - 4ac))/(2a)`

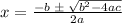
For the given quadratic equation
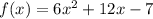`f(x)=6x^2+12x-7`, we have:

a = 6, b = 12, and c = -7

`x = (-(12)\; \pm \;√((12)^2 - 4(6)(-7)))/(2(6))\\\\x = (-(12)\; \pm \;√(144 + 168))/(12)\\\\x = (-12\; \pm \;√(312))/(12)\\\\x = (-12\; \pm \;√(13 * 24))/(12)\\\\x = -1 \;\pm \;\sqrt{(13)/(6) } \\\\x = -1 \;- \;\sqrt{(13)/(6) } \;and\;x = -1 \;+ \;\sqrt{(13)/(6) }`