Question

The average number of pounds of sliced ham ordered per customer at the deli where Dennis used to work was 1.4, but at his new job, the average of the 32 people who have ordered ham so far is 1.5 pounds, with a standard deviation of 0.3 pounds. a) Write the null and alternative hypotheses to test if the average amount of ham bought is higher at the new store. , b) For find the rejection region in terms of z. [Write your answer with 2 decimal places.] c) What test statistic corresponds to an of 1.5 pounds? [Round your answer to 2 decimal places.] d) Should you reject the null hypothesis?

Answer 1

(a) Null Hypothesis,
`H_0` :
`\mu`
`\leq` 1.4 pounds

Alternate Hypothesis,
`H_A` :
`\mu` > 1.4 pounds

(b) If the test statistics is more than the critical value of t at 31 degree of freedom, then we will reject our null hypothesis.

(c) The value of t test statistics is 1.886.

(d) We conclude that the average amount of ham bought is higher at the new store.

Explanation:

We are given that the average number of pounds of sliced ham ordered per customer at the deli where Dennis used to work was 1.4, but at his new job, the average of the 32 people who have ordered ham so far is 1.5 pounds, with a standard deviation of 0.3 pounds.

Let
`\mu` = average amount of ham bought at the new store.

So, Null Hypothesis,
`H_0` :
`\mu`
`\leq` 1.4 pounds {means that the average amount of ham bought is lesser than or equal to 1.4 pounds at the new store}

Alternate Hypothesis,
`H_A` :
`\mu` > 1.4 pounds {means that the average amount of ham bought is higher at the new store}

The test statistics that would be used here One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample average of ham ordered = 1.5 pounds

s = sample standard deviation = 0.3 pounds

n = sample of people = 32

So, test statistics =
`(1.5-1.4)/((0.3)/(√(32) ) )` ~
`t_3_1`

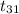
= 1.886

The value of t test statistics is 1.886.

Since, in the question we are not given with the level of significance so we assume it to be 5%. Now, at 5% significance level the t table gives critical value of 1.6955 at 31 degree of freedom for right-tailed test.

Since our test statistics is more than the critical values of t as 1.886 > 1.6955, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the average amount of ham bought is higher at the new store.