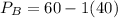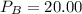Answer:
Market A:
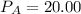
Market B:
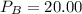
Step-by-step explanation:
Market A:
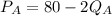 ........................ (1)
........................ (1)
Market B:
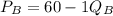 ........................ (2)
........................ (2)
MC = m = 20 ............................................... (3) for both markets
For Market A:
Profit maximizing price can be obtained when
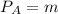
Therefore, we have:
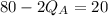

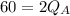
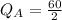
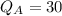
Substituting 50 for
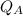 in equation (1), we have:
in equation (1), we have:
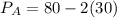

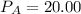
For Market B:
Profit maximizing price can be obtained when
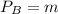
Therefore, we have:
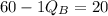
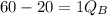
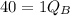
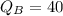
Substituting 80 for
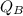 in equation (2), we have:
in equation (2), we have: