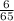Answer:
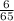
Explanation:
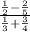
Let's solve each separately.
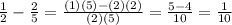
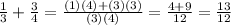
This leaves the fraction as;
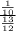
To get rid of the fraction in the denominator, multiply by its reciprocal. The reciprocal of a fraction is the same fraction but inverted.
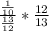
This will eliminate the denominator, leaving the fraction like;
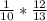
12 and 10 can be simplified.
12/2=6
10/2=5
Our new fraction would be;
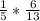
Multiply;