Question

The rotor of an electric motor has rotational inertia Im = 4.36 x 10-3 kg·m2 about its central axis. The motor is used to change the orientation of the space probe in which it is mounted. The motor axis is mounted along the central axis of the probe; the probe has rotational inertia Ip = 6.07 kg·m2 about this axis. Calculate the number of revolutions of the rotor required to turn the probe through 30.6° about its central axis.

Answer 1

The number of revolutions of the rotor required to turn the probe is 118 revolutions

Step-by-step explanation:

Given;

rotational inertia of the electric motor, Im = 4.36 x 10⁻³ kg·m²

rotational inertia of the probe, Ip = 6.07 kg·m²

the angular position of the probe, θ = 30.6°

From the principle of conservation of angular momentum;

`I_m \omega _m = I_p \omega _p \\\\Also;\\\\I_m \theta _m = I_p \theta _p`

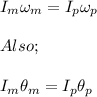
where;

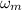`\omega _m` is the angular velocity of the electric motor

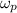`\omega _p` is the angular velocity of the probe

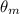`\theta _m` is the angular position of the electric motor

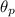`\theta _p` is the angular position of the probe

`\theta _m = (I_p \theta_p)/(I_m) \\\\\theta _m = (6.07* 30.6^o)/(4.36*10^(-3)) = 42601.4^o`

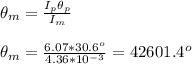
360° = One revolution

42601.4° = ?

Divide 42601.4° by 360°

= 118 revolutions

Therefore, the number of revolutions of the rotor required to turn the probe is 118 revolutions