 is a geometric sequence, which means consecutive terms occur in a fixed ratio. In other words,
is a geometric sequence, which means consecutive terms occur in a fixed ratio. In other words,
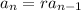
for some fixed number
 .
.
Using this rule, we have

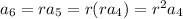
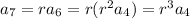
So, given that
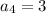 and
and
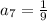 , we have
, we have
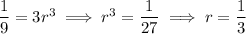
We can write
 in terms of
in terms of
 :
:

(notice how the subscript and exponent add up to
 ) so the sequence is given by the explicit rule
) so the sequence is given by the explicit rule
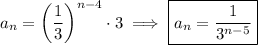
Incidentally, we can pull out the first term from this sequence by plugging in
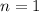 to find
to find
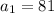 .
.
Next, if
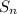 denotes the
denotes the
 th partial sum of the sequence, then
th partial sum of the sequence, then
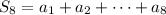
For geometric sequences, we can replace
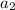 through
through
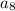 with terms containing
with terms containing
 :
:
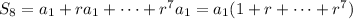
Multiply both sides by
 :
:
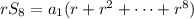
Subtract
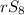 from
from
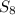 ; a bunch of terms cancel and we're left with
; a bunch of terms cancel and we're left with
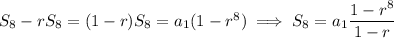
For the sequence at hand, plug in
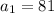 and
and
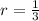 . Then
. Then
