Question

How can you tell if something is quadratic from a table?

Answer 1

Suppose you have a table like this one:

`\begin{array}cx&-3&-2&-1&0&1&2&3\\x^2&9&4&1&0&1&4&9\end{array}`

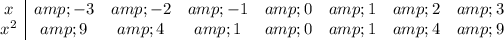
Notice how the difference between the consecutive squares is a sequence of odd numbers:

4 - 9 = -5

1 - 4 = -3

0 - 1 = -1

1 - 0 = 1

4 - 1 = 3

9 - 4 = 5

Notice also how the differences between *these* differences is fixed. That is, the second-order differences are

-3 - (-5) = 2

-1 - (-3) = 2

1 - (-1) = 2

3 - 1 = 2

5 - 3 = 2

A sequence of fixed second-order differences indicates a function has quadratic behavior.

Here's another example, where the function is unknown. Consider the sequence,

22, 11, 4, 1, 2, 7, 16

The first-order differences are

-11, -7, -3, 1, 5, 9

and the second-order differences are

4, 4, 4, 4, 4

So this sequence is also quadratic.