Question

Ignacio is curious about the average age of cars in the commuter lot at Mis large university. He takes a random

sample of 16 cars and finds that their average age is 2 = 14.5 years and their standard deviation is 8, = 4.6
years. The distribution of ages in the sample was roughly symmetric with no obvious outliers.
Based on this sample, which of the following is a 90% confidence interval for the mean age of cars (in years) in
this commuter lot?

Answer 1

12.48, 16.52

Explanation:

Took it on Khan

Answer 2

Between 12.614 years and 16.386 years

Explanation:

Given that:

Mean age (μ) = 14.5 years, standard deviation (σ) = 4.6 years, number o sample (n) and the confidence interval (c) = 90% = 0,9

α = 1 -c = 1 -0.9 = 0.1

`(\alpha )/(2) = (0.1)/(2) = 0.05`

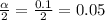
The z score of
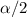`\alpha /2` is the same as the z score of 0.45 (0.5 - 0.05). This can be gotten from the probability distribution table. Therefore:

`z_(0.05)=1.64`

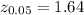
The margin of error (e) =
`z_(0.05)(\sigma)/(√(n) )` =
`1.64*(4.6)/(√(16) )=1.886`

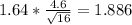
The interval = μ ± e = 14.5 ± 1.886 = (12.614 ,16.386)