Question

A survey reported in Time magazine included the question ‘‘Do you favor a federal law requiring a day waiting period to purchase a gun?" Results from a random sample of US citizens showed that of the men who were surveyed supported this proposed law while of the women sampled said ‘‘yes". Use this information to find a confidence interval for the difference in the two proportions, , where is the proportion of men who support the proposed law and is the proportion of women who support the proposed law.

Answer 1

The 90% confidence interval for the difference between proportions is (-0.260, -0.165).

Explanation:

The question is incomplete. The complete question is:

"A survey reported in Time magazine included the question ‘‘Do you favor a federal law requiring a 15 day waiting period to purchase a gun?” Results from a random sample of US citizens showed that 318 of the 520 men who were surveyed supported this proposed law while 379 of the 460 women sampled said ‘‘yes”. Use this information to find a 90% confidence interval for the difference in the two proportions, pm - pw. Subscript pm is the proportion of men who support the proposed law and pw is the proportion of women who support the proposed law. (Round answers to 3 decimal places.)"

We want to calculate the bounds of a 90% confidence interval.

For a 90% CI, the critical value for z is z=1.645.

The sample of men, of size nm=-0.26 has a proportion of pm=0.612.

`p_m=X_m/n_m=318/520=0.612`

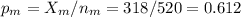
The sample 2, of size nw= has a proportion of pw=0.824.

`p_w=X_w/n_w=379/460=0.824`

The difference between proportions is (pm-pw)=-0.212.

`p_d=p_m-p_w=0.612-0.824=-0.212`

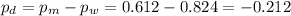
The pooled proportion, needed to calculate the standard error, is:

`p=(X_m+X_w)/(n_m+n_w)=(318+379)/(520+460)=(697)/(980)=0.711`

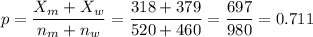
The estimated standard error of the difference between means is computed using the formula:

`s_(pm-pw)=\sqrt{(p(1-p))/(n_m)+(p(1-p))/(n_w)}=\sqrt{(0.711*0.289)/(520)+(0.711*0.289)/(460)}\\\\\\s_(pm-pw)=√(0.00039+0.00045)=√(0.001)=0.029`

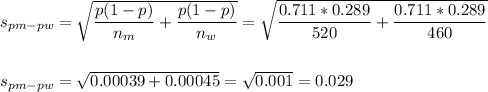
Then, the margin of error is:

`MOE=z \cdot s_(pm-pw)=1.645\cdot 0.029=0.0477`

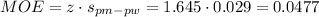
Then, the lower and upper bounds of the confidence interval are:

`LL=(p_1-p_2)-z\cdot s_(p1-p2) = -0.212-0.0477=-0.260\\\\UL=(p_1-p_2)+z\cdot s_(p1-p2)= -0.212+0.0477=-0.165`

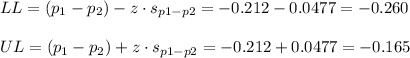
The 90% confidence interval for the difference between proportions is (-0.260, -0.165).