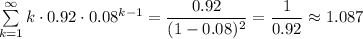Question

Here is data on the flow of students through a school.70% of freshmen pass and become sophomores, 20% fail and repeat as freshmen, 10% drop out80% of sophomores pass and become juniors, 10% fail and repeat as sophomores, 10% drop out80% of juniors pass and become seniors, 10% fail and repeat as juniors, 10% drop out82% of seniors pass and graduate, 8% fail and repeat as seniors, 10% drop outTreat this as a 6-state Markov chain with "graduated" and "dropped out" being absorbing states. Use an appropriate matrix tool to answer the following questions. (Give your answers correct to 3 decimal places.)(a) What fraction of freshmen graduate within 4 years?(b) What fraction of freshmen graduate within 5 years?(c) What fraction of freshmen eventually graduate?(d) What fraction of juniors eventually graduate?(e) Assume that a student enters the school as a senior. What is the expected value for the number of years that person will spend in school before either graduating or dropping out?

Answer 1

(a) 0.367

(b) 0.544

(c) 0.616

(d) 0.792

(e) 1.087

Explanation:

The transition matrix T multiplying the vector ...

{freshmen, sophomores, juniors, seniors, graduates, dropouts}

can be written as

`T=\left[\begin{array}{cccccc}0.2&0&0&0&0&0\\0.7&0.1&0&0&0&0\\0&0.8&0.1&0&0&0\\0&0&0.8&0.08&0&0\\0&0&0&0.82&1&0\\0.1&0.1&0.1&0.1&0&1\end{array}\right]`

(a) Then the 4th power of this matrix (1st attachment) will tell the number of freshmen graduating in 4 years. That will be ...

`(T^4)_(5,1)=0.367360\approx 0.367`

__

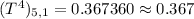
(b) Then the 5th power of this matrix (2nd attachment) will tell the number of freshmen graduating in 5 years. That will be ...

`(T^5)_(5,1)=0.543693\approx 0.544`

__

(c) The Nth power of matrix T as N approaches infinity (3rd attachment) will tell the numbers of students of each class who eventually graduate. For freshmen, that fraction is ...

`(T^(\infty))_(5,1)=0.616210\approx 0.616`

__

(d) As in part (c), the desired fraction is ...

`(T^(\infty))_(5,3)=0.792271\approx 0.792`

__

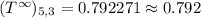
(e) The expected number of years spent in school is the sum of the products of time in school and the probability of taking that time. The expected value in years is ...

`\sum\limits_(k=1)^(\infty){k\cdot 0.92\cdot0.08^(k-1)}=(0.92)/((1-0.08)^2)=(1)/(0.92)\approx 1.087`