Question

The electric cooperative needs to know the mean household usage of electricity by its non-commercial customers in kWh per day. Assume that the population standard deviation is 2.3 kWh. The mean electricity usage per family was found to be 15.7 kWh per day for a sample of 1731 families. Construct the 99% confidence interval for the mean usage of electricity. Round your answers to one decimal place.

Answer 1

`15.7-2.58(2.3)/(√(1731))=15.6`

`15.7+2.58(2.3)/(√(1731))=15.8`

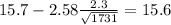
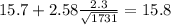
We are 99% confident that the true mean of electricity comsumption is between (15.6 and 15.8) kWh

Explanation:

Information provided

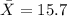`\bar X= 15.7` represent the sample mean for the usage of electricity

`\mu` population mean (variable of interest)

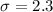`\sigma= 2.3` represent the population standard deviation

n=1731 represent the sample size

Confidence interval

The confidence interval for the mean is given by the following formula if we know the population deviation:

`\bar X \pm z_(\alpha/2)(\sigma)/(√(n))` (1)

The Confidence level provided is 0.99 or 95%, the value of significance is
`\alpha=0.01` and
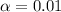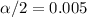`\alpha/2 =0.005`, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-NORM.INV(0.005,0,1)".And we see that
`z_(\alpha/2)=2.58`

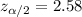
And replacing we got:

`15.7-2.58(2.3)/(√(1731))=15.6`

`15.7+2.58(2.3)/(√(1731))=15.8`

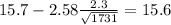
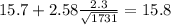
We are 99% confident that the true mean of electricity comsumption is between (15.6 and 15.8) kWh