Question

Amy and Betty run in opposite directions on a circular track, starting at diametrically opposite points. They first meet after Amy has run 120 meters. They next meet after Betty has run 180 meters past their first meeting point. Each girl runs at a constant speed. What is the length of the track in meters?

Answer 1

420 meters

Explanation:

The first thing we must do is understand the exercise, the first thing is that they go in opposite directions, one goes clockwise and the other goes counter-clockwise.

We can interpret that one is in the "beginning" of the track and the other is in the "middle". Let's say that the length of the track is "x"

Now, their first meeting is when Amy has traveled 120 meters, which means that how Betty is in the middle would be x/2 - 120, which she traveled. We are told that Betty traveled 180 meters after that meeting point which means, how did she start "beginning" but that beginning can also be seen as the end, that is, distance x, traveled x - 180.

We can do the following proportion:

`(120)/(x-180)=((x)/(2)-120)/(180)`

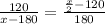
120*180 = (x/2 -120)*(x-180)

in resolving:

x^2-420*x+43200=43200

x^2 -420*x = 0

x*(x -420)=0

x - 420 = 0

x = 420

Therefore the circular track has a length of 420 meters