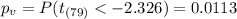Question

Fluoxetine, a generic anti-depressant, claims to have, on average, at least 20 milligrams of active ingredient. An independent lab tests a random sample of 80 tablets and finds the mean content of active ingredient in this sample is 18.7 milligrams with a standard deviation of 5 milligrams. If the lab doesn't believe the manufacturer's claim, what is the approximate p-value for the suitable test

Answer 1

`t=(18.7-20)/((5)/(√(80)))=-2.326`

`df=n-1=80-1=79`

`p_v =P(t_((79))<-2.326)=0.0113`

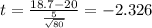
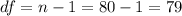
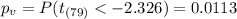
Explanation:

Information given

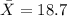`\bar X=18.7` represent the sample mean for the content of active ingredient

`s=5` represent the sample standard deviation for the sample

`n=80` sample size

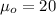`\mu_o =20` represent the value that we want to test

t would represent the statistic

`p_v` represent the p value for the test

System of hypothesis

We need to conduct a hypothesis in order to check if the true mean for the active agent is at least 20 mg, the system of hypothesis would be:

Null hypothesis:
`\mu \geq 20`

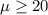
Alternative hypothesis:
`\mu < 20`

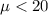
The statistic would be:

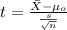`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

Now we can calculate the statistic:

`t=(18.7-20)/((5)/(√(80)))=-2.326`

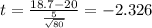
P value

The degrees of freedom are calculated like this:

`df=n-1=80-1=79`

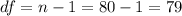
Since is a one left tailed test the p value would be:

`p_v =P(t_((79))<-2.326)=0.0113`