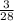Question

A jar contains five blue marbles and three red marbles. Suppose you choose a marble at​ random, and do not replace it. Then you choose a second marble. Find the probability of the following event.

Both of the selected marbles are red.

Answer 1

The probability that both of the selected marbles are red is
`(3)/(28)`

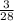
Explanation:

Given

Number of red marbles = 3

Number of blue marbles = 5

Required

Probability of selecting two red marbles (without replacement).

First, we need to get the total number of marbles

Total = Red Marbles + Blue Marbles

Total = 3 + 5

Total = 8

Probability is calculated by: Number of required outcome divided by number of possible outcome.

Since there are 3 red marbles out of a total of 8 marbles;

The probability that the first marble you selected is red is 3/8

From the question, you didn't return the marble back to the container.

This means that, there are 2 red marbles and a total of 7 marbles left in the container.

So, the probability that the next marble selected is red is 2/7

Let P(R and R) represent the probability of selecting two red marbles.

This is calculated by multiplying the probability of picking the first red marble and the second red marble.

Hence,

P(R and R) =
`(3)/(8) * (2)/(7)`

P(R and R) =
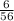`(6)/(56)` --- Reduce to lowest term

P(R and R) =
`(3)/(28)`

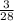
Hence, the probability that both of the selected marbles are red is
`(3)/(28)`