Question

A circular fountain has 132 feet of railing around it. What is the area of the fountain, Use 3.14 for π.

Answer 1

1387.2 ft² (nearest tenth)

Explanation:

Formulae

• Circumference of a circle =
  `2 \pi r`
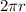
• Area of a circle =
  `\pi r^2`

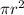
(where r is the radius of the circle)

The railing of the circular fountain is the circumference of a circle.

The area of the fountain is the area of a circle.

First, find the radius by using the circumference formula:

Given:

• circumference = 132 ft

`\implies 132=2 \pi r`

`\implies r=(132)/(2 \pi)=(66)/(\pi)`

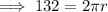
Now input the found value of r into the formula for the area of a circle:

`\begin{aligned}\implies \textsf{Area} & =\pi \left((66)/(\pi)\right)^2\\\\ & = (4356)/(\pi)\\\\ & = (4356)/(3.14)\\\\ & = 1387.261146...\\\\ & = 1387.3 \: \sf ft^2\:(nearest\:tenth)\end{aligned}`