Question

The owner of the pizza chain wants to monitor the total weight of pepperoni. Suppose that for pizzas in this population, the weights have a mean of 250g and a standard deviation of 4g. Management takes a random sample of 64 of these pizzas and calculates the mean weight of the pepperoni on the pizzas. Assume that the pizzas in the sample are independent. What is the probability that the mean weight of the pepperoni from the sample of 64 pizzas is greater than 251g

Answer 1

The probability that the mean weight of the pepperoni from the sample of 64 pizzas is greater than 251 g is 0.02275.

Explanation:

We are given that the owner of the pizza chain wants to monitor the total weight of pepperoni. Suppose that for pizzas in this population, the weights have a mean of 250 g and a standard deviation of 4 g.

Management takes a random sample of 64 of these pizzas.

Let
`\bar X` = sample mean weight of the pepperoni.

The z score probability distribution for sample mean is given by;

Z =
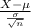`(X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean weight = 250 g

`\sigma` = standard deviation = 4 g

n = sample of pizzas = 64

Now, the probability that the mean weight of the pepperoni from the sample of 64 pizzas is greater than 251 g is given by = P(
`\bar X` > 251 g)

P(
`\bar X` > 251 g) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
`(251-250)/((4)/(√(64) ) )` ) = P(Z > 2) = 1 - P(Z
`\leq` 2)

= 1 - 0.97725 = 0.02275

The above probabilities is calculated by looking at the value of x = 2 in the z table which has an area of 0.97725.

Hence, the probability that the mean weight of the pepperoni from the sample of 64 pizzas is greater than 251 g is 0.02275.