Answer:
The velocity that will be needed for the model and prototype to be similar is 108.97m/s
Step-by-step explanation:
length of Torpedo = 3m
diameter,

velocity of sea water,
 = 10m/s
= 10m/s
dynamic viscosity of sea water, η
 = 0.00097 Ns/m²
= 0.00097 Ns/m²
density of sea water, ρ
 = 1023 kg/m³
= 1023 kg/m³
Scale model = 1:15
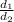 =
=

Cross multiplying: d
 =
=
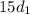 = 15 ×0.5 = 7.5m
= 15 ×0.5 = 7.5m
Let:
velocity of air,
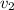
viscosity of air, η
 = 0.000186Ns/m²
= 0.000186Ns/m²
density of air, ρ
 = 1.2 kg/m³
= 1.2 kg/m³
For the model and the prototype groups to be equal, Non-dimensional groups should be equal.
Reynold's number: (ρ
 ×
×
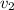 ×d
×d
 )/η
)/η
 = (ρ
= (ρ
 ×
×
 ×d
×d
 )/η
)/η

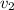 = η
= η
 /(ρ
/(ρ
 ×d
×d
 ) × (ρ
) × (ρ
 ×
×
 ×d
×d
 )/η
)/η

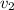 =
=
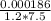 ×
×
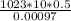 , note: * means multiplication
, note: * means multiplication
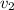 = 108.97m/s
= 108.97m/s
velocity that will be needed for the model and prototype to be similar = 108.97m/s