Answer:
Area of the square base: 144 in²
Area of each triangular face: 66 in²
Amount of paint needed: 408 in²
Explanation:
We basically want to find the surface area of this square pyramid.
First, find the areas of the 4 triangular sides. The area of a triangle is denoted by:
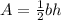 , where b is the base and h is the height.
, where b is the base and h is the height.
Here, the base coincides with the side length of the square, so b = 12. The height is 11, so h = 11. Plug these in:
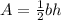
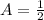 * 12 * 11 = 66 inches squared
* 12 * 11 = 66 inches squared
Each triangular face is thus 66 inches squared.
Since there are 4 triangles, multiply 66 by 4: 66 * 4 = 264 inches squared
Now, find the area of the square base. The area of a square is: A = s * s, where s is the side length. Here, the side length is 12, so s = 12. Plug this into the equation:
A = s * s
A = 12 * 12 = 144
So, the square base is 144 inches squared.
Finally, add 144 to 264 to get the total area Gabriel needs to paint:
144 + 264 = 408 inches squared