Question

Larry Mitchell invested part of gis 35,000 advance at 3% annual simple interest and the rest at 2% annual simple interest. If his total yearly interest from both accounts was $900, find the amount invested at each rate.

Answer 1

He invested $20000 for 3% rate and $15000 for 2% rate.

Step-by-step explanation:.

Let the 3% rate be for Account A and the 2% rate for Account B.

From the question, we know that the Principal from both accounts must add up to $35000

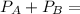`P_A + P_B =` 35000 ________________________ (1)

We also know that the interest from both accounts add up to $900

`I_A + I_B = $900`________________________(2)

The Interest from Account A (R = 3%, T = 1) is:

`I_A = (P_A *R*T)/(100)`

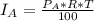
This implies that:

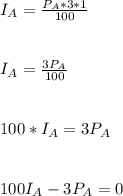`I_A = (P_A *3*1)/(100)\\\\\\I_A = (3P_A)/(100) \\\\\\100*I_A = 3P_A\\\\\\100I_A - 3P_A = 0`________________________(3)

The Interest from Account B (R = 2%, T = 1) is:

`I_B = (P_B *R*T)/(100)`

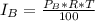
This implies that:

`I_B = (P_B *2*1)/(100)\\\\\\I_B = (2P_B)/(100) \\\\\\100*I_B = 2P_B\\\\\\100I_B - 2P_B = 0`_____________________________(4)

From (1),

`P_B = 35000 - P_A`

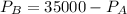
Putting this in (4)

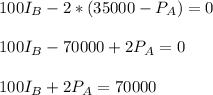`100I_B - 2*(35000 - P_A) = 0\\\\100I_B -70000 + 2P_A = 0\\\\100I_B +2P_A = 70000`________________(5)

From (2):

`I_A = 900 - I_B`

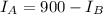
Putting this in (3):

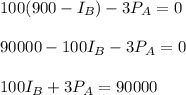`100(900 - I_B) - 3P_A = 0\\\\90000 - 100I_B - 3P_A = 0\\\\100I_B +3P_A = 90000`_______________________(6)

(5) and (6) are simultaneous equations, hence, we can solve them:

`100I_B +3P_A = 90000\\\\100I_B + 2P_A = 70000`

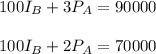
Subtracting (5) from (6):

`3P_A - 2P_A = 90000 - 70000`

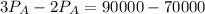
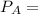`P_A =` $20000

Hence:

`P_B = 35000 - 20000\\\\`

`P_B =` $15000

Also:

`100I_B + 3P_A = 90000\\\\100I_B + (3 * 20000) = 90000\\\\100I_B + 60000 = 90000\\\\\\100I_B = 90000 - 60000\\\\100I_B = 30000`

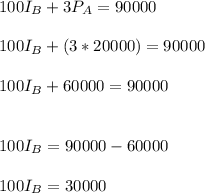
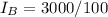`I_B = 3000/100` = $300

Hence:

`I_A = 900 - 300\\\\`

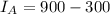
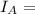`I_A =` $600

Hence, Larry invested $20000 at 3% annual interest and got $600 interest. He also invested $15000 at 2% annual interest and got $300.