Question

(3 points) Two friends went fishing. Hilda caught a 16 inch rainbow trout and Bran caught a 23 inch brown trout. Suppose rainbow trout have a mean length of 12 inches with a standard deviation 4 inches. Suppose brown trout have a mean length of 20 inches with a standard deviation of 5 inches. Which fish is longer relative to the type of fish? Make sure to show your work!

Answer 1

We are assuming here that the lengths of rainbow trout and brown trout follow a normal distribution, that is, both lengths are normally distributed (which is reasonable for this kind of random variable in populations, like the heights in humans, for example).

Answer:

The rainbow trout resulted longer relative to the corresponding type of fish, that is, one standard deviation above the mean or longer than the 84.134% of the population for rainbow trouts because the brown trout resulted in 0.6 standard deviations above the population for brown trouts (or 72.575% above them).

Explanation:

Because both types of fish come from different species, they cannot be fairly compared using the normal distribution of each fish.

Instead, we can compare them if we "transform" these raw data into z-scores in a way that we can use standardized values to determine how far from the mean are the lengths for each fish.

In other words, we have to remember that z-scores tell us the distance of a raw value from the population mean in standard deviations units, no matter the parameters of the normal distribution they coming from. A positive value for the z-score tells us that the raw score is above the population mean, whereas a negative value tells us that the raw score is below it.

We have to remember that the normal distribution is determined by two parameters, namely, the population mean and the population standard deviation.

In the question, we have two lengths coming from two different normal distributions. We can transform them into standardized values so that we can use the standard normal distribution, and then obtain how far from the mean are the lengths for each fish and the percentile that corresponds to this z-score.

The formula for the z-score is

`\\ z = (x - \mu)/(\sigma)` [1]

Where

x is the raw score. In this case, we have two. One is the length of the rainbow trout (16 inches) and the brown trout length (23 inches).

`\\ \mu` is the population mean for each normal distribution. We also have two. For the rainbow trout mean length, we have a mean of 12 inches, and a mean length of 20 inches for the brown trout.

`\\ \sigma` is the population standard deviation for each normal distribution. A standard deviation for the rainbow trout of 4 inches, and a standard deviation of 5 inches for the brown trout.

Having all this information at hand, we can proceed to solve the question.

Z-score for rainbow trout

For this case, we have

x = 16 inches.

`\\ \mu = 12` inches.

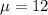`\\ \sigma = 4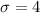` inches.

Using formula [1]

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (16 - 12)/(4)`

`\\ z = (4)/(4)`

`\\ z = 1`

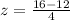
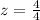
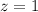
That is, the length of the rainbow trout caught by Hilda is one standard deviation above the mean. If we consult a cumulative standard normal table, we have that

`\\ P(z<1) = 0.84134`

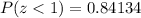
In words, the length for the fish that Hilda caught is, approximately, above than 84.134% of the population for rainbow trouts (one standard deviation above the population mean).

Z-score for brown trout

We can proceed in the same way as we did with the previous case.

For this case, we have

x = 23 inches.

`\\ \mu = 20` inches.

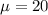`\\ \sigma = 5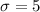` inches.

Using formula [1]

`\\ z = (23 - 20)/(5)`

`\\ z = (3)/(5)`

`\\ z = 0.6`

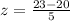
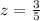
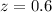
That is, the length of the brown trout caught by Bran is 0.6 standard deviations units above the mean. With this value at hand, we can conclude that this fish is smaller relative to the type of fish (brown trout) than the rainbow trout caught by Hilda. We can confirm this using the standard normal table:

`\\ P(z<0.6) = 0.72575`

In words, the length for the fish that Bran caught is, approximately, above than 72.575% of the population for brown trouts (or the length of 72.575% of the population for brown trout are below the length of the brown trout caught by Bran).

In conclusion, the rainbow trout resulted longer relative to the corresponding type of fish, that is, one standard deviation above the mean or longer than the 84.134% of the population for rainbow trouts, because the brown trout resulted in 0.6 standard deviations above the population for brown trouts (or 72.575% above them).

In the graph below, a standard normal distribution (mean = 0, standard deviation = 1), we can confirm the previous result (the red color for the rainbow trout, and the blue color for the brown trout).