Question

A cannon of mass 6.43 x 103 kg is rigidly bolted to the earth so it can recoil only by a negligible amount. The cannon fires a 73.8-kg shell horizontally with an initial velocity of 503 m/s. Suppose the cannon is then unbolted from the earth, and no external force hinders its recoil. What would be the velocity of a shell fired from this loose cannon

Answer 1

The velocity of the shell when the cannon is unbolted is 500.14 m/s

Step-by-step explanation:

Given;

mass of cannon, m₁ = 6430 kg

mass of shell, m₂ = 73.8-kg

initial velocity of the shell, u₂ = 503 m/s

Initial kinetic energy of the shell; when the cannon is rigidly bolted to the earth.

K.E = ¹/₂mv²

K.E = ¹/₂ (73.8)(503)²

K.E = 9336032.1 J

When the cannon is unbolted from the earth, we apply the principle of conservation of linear momentum and kinetic energy

change in initial momentum = change in momentum after

0 = m₁u₁ - m₂u₂

m₁v₁ = m₂v₂

where;

v₁ is the final velocity of cannon

v₂ is the final velocity of shell

`v_1 = (m_2v_2)/(m_1)`

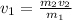
Apply the principle of conservation kinetic energy

`K = (1)/(2)m_1v_1^2 + (1)/(2)m_2v_2^2\\\\K = (1)/(2)m_1((m_2v_2)/(m_1))^2 + (1)/(2)m_2v_2^2\\\\K = (1)/(2)m_2v_2^2((m_2)/(m_1)) + (1)/(2)m_2v_2^2 \\\\K = (1)/(2)m_2v_2^2 ((m_2)/(m_1) + 1)\\\\2K = m_2v_2^2 ((m_2)/(m_1) + 1)\\\\v_2^2 = (2K)/(M_2((m_2)/(m_1) + 1)) \\\\v_2^2 = (2*9336032.1)/(73.8((73.8)/(6430) + 1))\\\\`

`v_2^2 = 250138.173\\\\v_2 = √(250138.173) \\\\v_2 = 500.14 \ m/s`

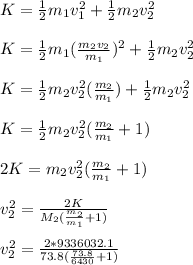
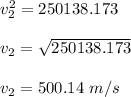
Therefore, the velocity of the shell when the cannon is unbolted is 500.14 m/s