Given Information:
Mean of fast food meals per week = μ = 6.76
Standard deviation of fast food meals per week = σ = 1.31
Confidence level = 90%
Margin of error = 0.070
Required Information:
Sample size = n = ?
Answer:
Sample size ≈ 948
Explanation:
We know that margin of error is given by
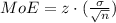
Where n is the required sample size, z is the value of z-score corresponding to 90% confidence level and σ is the standard deviation.
Re-arranging the above equation for n yields,
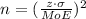
For 90% confidence level the corresponding z-score is 1.645
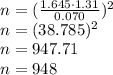
Therefore, a minimum sample size of 948 meals is required to ensure a margin of error no more than 0.070.