Answer:
a) q' = 351.22 W/m
b) q'_total = 1845.56 W / m
c) q'_loss = 254.12 W/m
Step-by-step explanation:
Given:-
- The diameter of the steam line, d = 100 mm
- The surface emissivity of steam line, ε = 0.8
- The temperature of the steam, Th = 150°C
- The ambient air temperature, T∞ = 20°C
Find:-
(a) Calculate the rate of heat loss per unit length for a calm day.
Solution:-
- Assuming a calm day the heat loss per unit length from the steam line ( q ' ) is only due to the net radiation of the heat from the steam line to the surroundings.
- We will assume that the thickness "t" of the pipe is significantly small and temperature gradients in the wall thickness are negligible. Hence, the temperature of the outside surface Ts = Th = 150°C.
- The net heat loss per unit length due to radiation is given by:
q' = ε*σ*( π*d )* [ Ts^4 - T∞^4 ]
Where,
σ: the stefan boltzmann constant = 5.6703 10-8 (W/m2K4)
Ts: The absolute pipe surface temperature = 150 + 273 = 423 K
T∞:The absolute ambient air temperature = 20 + 273 = 293 K
Therefore,
q' = 0.8*(5.6703 10-8)*( π*0.1 )* [ 423^4 - 293^4 ]
q' = (1.4251*10^-8)* [ 24645536240 ]
q' = 351.22 W / m ... Answer
Find:-
(b) Calculate the rate of heat loss on a breezy day when the wind speed is 8 m/s.
Solution:-
- We have an added heat loss due to the convection current of air with free stream velocity of U∞ = 8 m/s.
- We will first evaluate the following properties of air at T∞ = 20°C = 293 K
Kinematic viscosity ( v ) = 1.5111*10^-5 m^2/s
Thermal conductivity ( k ) = 0.025596
Prandtl number ( Pr ) = 0.71559
- Determine the flow conditions by evaluating the Reynold's number:
Re = U∞*d / v
= ( 8 ) * ( 0.1 ) / ( 1.5111*10^-5 )
= 52941.56574 ... ( Turbulent conditions )
- We will use Churchill - Bernstein equation to determine the surface averaged Nusselt number ( Nu_D ):
![Nu_D = 0.3 + (0.62*Re_D^(1)/(2)*Pr^(1)/(3) )/([ 1 + ((0.4)/(Pr))^(2)/(3) ]^(1)/(4) )*[ 1 + ((Re_D)/(282,000))^(5)/(8) ]^(4)/(5) \\\\Nu_D = 0.3 + (0.62*(52941.56574)^(1)/(2)*(0.71559)^(1)/(3) )/([ 1 + ((0.4)/(0.71559))^(2)/(3) ]^(1)/(4) )*[ 1 + ((52941.56574)/(282,000))^(5)/(8) ]^(4)/(5) \\\\](https://img.qammunity.org/2021/formulas/engineering/college/6ux1228nhbpenvmjr7u3ski2y62gd8pj5c.png)
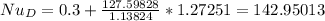
- The averaged heat transfer coefficient ( h ) for the flow of air would be:

- The heat loss per unit length due to convection heat transfer is given by:
q'_convec = h*( π*d )* [ Ts - T∞ ]
q'_convec = 36.58951*( π*0.1 )* [ 150 - 20 ]
q'_convec = 11.49493* 130
q'_convec = 1494.3409 W / m
- The total heat loss per unit length ( q'_total ) owes to both radiation heat loss calculated in part a and convection heat loss ( q_convec ):
q'_total = q_a + q_convec
q'_total = 351.22 + 1494.34009
q'_total = 1845.56 W / m ... Answer
Find:-
For the conditions of part (a), calculate the rate of heat loss with a 20-mm-thick layer of insulation (k = 0.08 W/m ⋅ K)
Solution:-
- To reduce the heat loss from steam line an insulation is wrapped around the line which contains a proportion of lost heat within.
- A material with thermal conductivity ( km = 0.08 W/m.K of thickness t = 20 mm ) was wrapped along the steam line.
- The heat loss through the lamination would be due to conduction " q'_t " and radiation " q_rad":

q' = ε*σ*( π*( d + 2t) )* [ Ts^4 - T∞^4 ]
Where,
T_o = T∞ = 20°C
T_s = Film temperature = ( Th + T∞ ) / 2 = ( 150 + 20 ) / 2 = 85°C
r_2 = d/2 + t = 0.1 / 2 + 0.02 = 0.07 m
r_1 = d/2 = 0.1 / 2 = 0.05 m
- The heat loss per unit length would be:
q'_loss = q'_rad - q'_cond
- Compute the individual heat losses:

Therefore,
q'_loss = 351.22 - 97.10
q'_loss = 254.12 W / m .... Answer
- If the wind speed is appreciable the heat loss ( q'_loss ) would increase and the insulation would become ineffective.