Answer:
Steve should use:
- 8.53 Inch of Wire to make the circle
- 43.47 Inches of Wire to make the Square.
Explanation:
Let Steve cut the wire so that the first piece has length x.
Therefore, the second piece will have a length of (52 - x).
The wire of length x is used to make a circle
Circumference of a Circle,
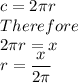
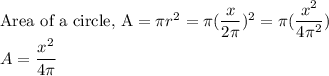
The wire of length (52-x) is used to make a square.

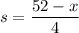
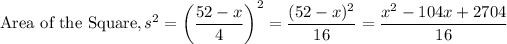
Total Area = Area of Circle + Area of Square
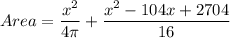
Let us simplify the expression
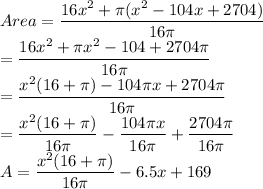
This is the function of a parabola which opens up.
To find where A is minimum, find the axis of symmetry.
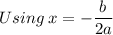

Steve should cut the wire so that the length of wire used to make a circle is 8.53 Inches.
Length of wire used to make the square =52-8.53=43.47 Inches