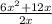Answer:
Part a)
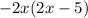
Part b)

Explanation:
Part a)
I first determined what each piece in the rectangular array meant.
Then I wanted to figure out the height and the base length.
I know
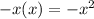 so that is why I put those purple
so that is why I put those purple
 's on top and purple
's on top and purple
 's down alongside for the
's down alongside for the
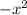 pieces. To get
pieces. To get
 when I already had
when I already had
 , I needed to multiply by -1 which is why there is a -1 along the top where those
, I needed to multiply by -1 which is why there is a -1 along the top where those
 pieces are.
pieces are.
So in the first question down the side of the box, we have
![-x+-x=-2x/tex]. </p><p>Along the the top we have [tex]x+x-1-1-1-1-1=2x-5](https://img.qammunity.org/2021/formulas/mathematics/high-school/vcxpwljssg5axn8i7ipuucebvjqwx8r418.png) .
.
To find the area of the rectangle, you multiply height by base.
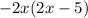 .
.
Part b)We have six
 's and twelve
's and twelve
 's. So that means the polynomial represented here is
's. So that means the polynomial represented here is
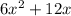 .
.
What happens if we divide that by
 .
.
Let's see: