Answer:
0.74
Explanation:
The standard deviation of a data set is the sqaure root of the variance, so first we must find the variance. The equation for variance is:
σ² =
![\frac{{(x_(1)-[x bar] )}^(2)+...+{(x_(n)-[x bar]) }^(2)}{n}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/oki92drq6bo8b9czsivj.png)
x = number in the data set
xbar = median of the data set
n = number of terms
Plugging in the given values, the equation for the variance of this number set is:
σ² =

Solving:
=
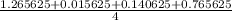
=
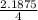
σ² = 0.546875
Since the standard devianation is the sqaure root of the variance, we'll sqaure 0.546875:
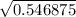
= 0.73950997288745
= 0.74 (rounded)
hope this helps!