We have been given an image of a circle. We are asked to find the measure of angle JKL.
We can see that angle JML is a central angle of our given circle, so measure of angle JML will be equal to measure of arc JL. So measure of angle JML will be 60 degrees.
We know that tangent of a circle is perpendicular to radius.
We can see that tangent KJ is tangent to circle at point J and tangent KL is tangent to circle at point L. This means that measure of angle KJM and angle KLM will be 90 degrees each.
We can see that JKLM is a quadrilateral. We know that all angles of a quadrilateral add up-to 360 degrees, so we can set an equation as:
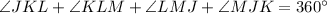

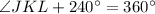
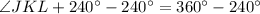

Therefore, measure of angle JKL is 120 degrees and option B is the correct choice.