Question

Every year, people in the US buy 2.7 billion boxes of breakfast cereal. A “typical” cereal box has dimensions of 2.5 inches by 7.75 inches by 11.75 inches. Imagine a warehouse that has a rectangular floor and that contains all the boxes of breakfast cereal bought in the US in one year. If the warehouse is 10 feet tall, what could the side lengths be? Is is possible to design a different sized cereal box to increase the amount of cereal in this warehouse?

Answer 1

a. The side lengths of the warehouse could be

Length = 7343.75 ft

Width = ‪4843.75 ft

b. No

Explanation:

a. Here we have

Thickness of box of breakfast cereal = 2.5 inches

Length of breakfast cereal = 11.75 inches

Width of breakfast cereal = 7.75 inches

Number of boxes = 2.7 × 10⁹

Size of warehouse

Height = 10 feet = 120 inches

Therefore, number of boxes the warehouse can take vertically is
`(120 \, in.)/(2.5 \, in./box) = 48 \, boxes`

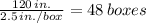
Therefore, the number of boxes to be arranged length wise and width wise is 2.7 × 10⁹ ÷ 48 = 56,250,000 boxes

If we arranged equal number of boxes length wise and wise, we have

√56,250,000 = 7500 boxes long and 7500 boxes wide

That is 7500 × 11.75 in = 88,125 in. ‪7343.75 ft long and

7500 × 7.75 = 58,125 in. = ‪4843.75 ft wide

Therefore, the side lengths could be

Length = 7343.75 ft

Width = ‪4843.75 ft

b. No since the dimensions of the warehouse is fixed and proportional to the dimensions the cereal box