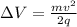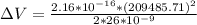Answer:
a
The speed of the particle is
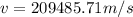
b
The potential difference is

Step-by-step explanation:
From the question we are told that
The mass of the particle is
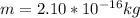
The charge on the particle is

The magnitude of the magnetic field is
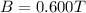
The magnetic flux is
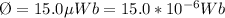
The magnetic flux is mathematically represented as
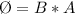
Where A is the the area mathematically represented as
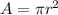
Substituting this into the equation w have
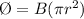
Making r the subject of the formula
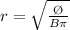
Substituting value

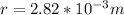
For the particle to form a circular path the magnetic force the partial experience inside the magnetic must be equal to the centripetal force of the particle and this is mathematically represented as
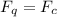
Where

and
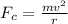
Substituting this into the equation above
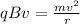
making v the subject
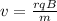
substituting values
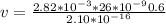
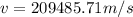
The potential energy of the particle before entering the magnetic field is equal to the kinetic energy in the magnetic field
This is mathematically represented as

Where
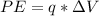
and
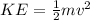
Substituting into the equation above
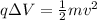
Making the potential difference the subject