Question

Ignoring those who said they weren't sure, there were 297 men asked, and 183 said yes, they had driven a car when they probably had too much alcohol. Does this provide statistically significant evidence that a majority of men in the population (that is, more than half) would say that they had driven a car when they probably had too much alcohol, if asked

Answer 1

`z=\frac{0.616-0.5}{\sqrt{(0.5(1-0.5))/(297)}}=3.998`

`p_v =2*P(z>3.998)=0.0000639`

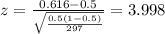
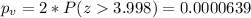
With the most common significance levels used
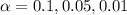`\alpha= 0.1, 0.05, 0.01` we see that the p value is lower than the significance level so then we have enough evidence to reject the null hypothesis and we can say that the true proportion is significantly higher than 0.5

Explanation:

Information given

n=297 represent the random sample of male taken

X=183 represent the men who said yes, they had driven a car when they probably had too much alcohol

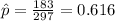`\hat p=(183)/(297)=0.616` estimated proportion of men who said yes, they had driven a car when they probably had too much alcohol

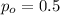`p_o=0.5` is the value that we want to test

z would represent the statistic (variable of interest)

`p_v` represent the p value (variable of interest)

Hypothesis to test

We need to conduct a hypothesis in order to test the claim that the majority of men in the population (that is, more than half) would say that they had driven a car when they probably had too much alcohol, and the system of hypothesis are:

Null hypothesis:
`p\leq 0.5`

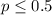
Alternative hypothesis:
`p > 0.5`

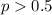
The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

After replace we got:

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.616-0.5}{\sqrt{(0.5(1-0.5))/(297)}}=3.998`

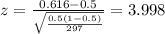
Decision

We have a right tailed test so then the p value would be:

`p_v =2*P(z>3.998)=0.0000639`

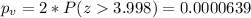
With the most common significance levels used
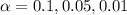`\alpha= 0.1, 0.05, 0.01` we see that the p value is lower than the significance level so then we have enough evidence to reject the null hypothesis and we can say that the true proportion is significantly higher than 0.5