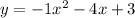Question

The line of symmetry of the parabola whose equation is y = ax^2 -4x + 3 is

x = -2. What is the value of "a"?

A. -2
B. -1
C. -1/2

Answer 1

B. -1

Explanation:

If we have a parabola whose equation is:

`y=ax^(2) +bx+c`

The line of symmetry is calculated as:

`x=(-b)/(2a)`

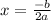
Now, we have the equation
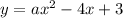`y=ax^(2)-4x+3` and the line of symmetry is
`x=-2`

Where:

`b=-4\\c=3`

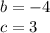
So, we can replace
`b` by -4 and
`x` by -2 and solve for
`a` using the following equation as:

`x=(-b)/(2a)\\-2=(-(-4))/(2a)\\-2(2)a=4\\-4a=4\\a=-1`

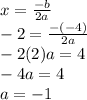
It means that the equation of the parabola is equal to:

`y=-1x^(2)-4x+3`