Answer:
The probability it will weigh between 2.95 and 3.1 ounces is 0.8186.
Explanation:
We are given that Whitney Gourmet Cat Food has determined the weight of their cat food can is normally distributed with a mean of 3 ounces and a standard deviation of 0.05 ounces.
Let X = weight of their cat food can
So, X ~ Normal(
 )
)
The z score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 3 ounces
= population mean = 3 ounces
 = standard deviation = 0.05 ounces
= standard deviation = 0.05 ounces
Now, the probability it will weigh between 2.95 and 3.1 ounces is given by = P(2.95 ounces < X < 3.1 ounces)
P(2.95 ounces < X < 3.1 ounces) = P(X < 3.1 ounces) - P(X
 2.95 ounces)
2.95 ounces)
P(X < 3.1 ounces) = P(
 <
<
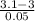 ) = P(Z < 2) = 0.97725
) = P(Z < 2) = 0.97725
P(X
 2.95 ounces) = P(
2.95 ounces) = P(


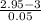 ) = P(Z
) = P(Z
 -1) = 1 - P(Z < 1)
-1) = 1 - P(Z < 1)
= 1 - 0.84134 = 0.15866
The above probabilities is calculated by looking at the value of x = 2 and x = 1 in the z table which has an area of 0.97725 and 0.84134 respectively.
Therefore, P(2.95 ounces < X < 3.1 ounces) = 0.97725 - 0.15866 = 0.8186
Hence, the probability it will weigh between 2.95 and 3.1 ounces is 0.8186.