Question

Assume that the Poisson distribution applies and that the mean number of hurricanes in a certain area is 6.7 per year. a. Find the probability​ that, in a​ year, there will be 4 hurricanes. b. In a 35​-year ​period, how many years are expected to have 4 ​hurricanes? c. How does the result from part​ (b) compare to a recent period of 35 years in which 3 years had 4 ​hurricanes? Does the Poisson distribution work well​ here?

Answer 1

a) 10.34% probability​ that, in a​ year, there will be 4 hurricanes.

b) 3.62 years are expected to have 4 ​hurricanes

c) Either 3 or 4 hurricanes(discrete number) are close to the mean of 3.62, which means that the Poisson distribution works well in this case.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

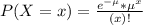
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

6.7 per year.

This means that
`\mu = 6.7`

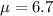
a. Find the probability​ that, in a​ year, there will be 4 hurricanes.

This is P(X = 4).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 4) = (e^(-6.7)*(6.7)^(4))/((4)!) = 0.1034`

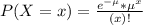
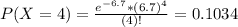
10.34% probability​ that, in a​ year, there will be 4 hurricanes.

b. In a 35​-year ​period, how many years are expected to have 4 ​hurricanes?

Each year, 0.1034 probability of 10 hurricanes.

In 35 years

35*0.1034 = 3.62

3.62 years are expected to have 4 ​hurricanes

c. How does the result from part​ (b) compare to a recent period of 35 years in which 3 years had 4 ​hurricanes? Does the Poisson distribution work well​ here?

Either 3 or 4 hurricanes(discrete number) are close to the mean of 3.62, which means that the Poisson distribution works well in this case.