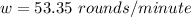Answer:
The angular velocity is
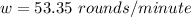
Step-by-step explanation:
From the question we are told that
The mass of the block is
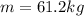
The of the pulley is
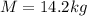
The radius of the pulley is
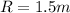
The radius of the cord around the pulley is
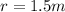
The distance of the block to the floor is
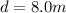
From the question we are told that the moment of inertia of the pulley is
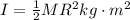
Substituting value
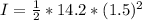
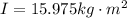
Using the Newtons law we can express the force acting on the vertical axis as
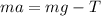
=>
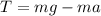
Now when the pulley is rotated that torque generated on the massless cord as a r result of the tension T and the radius of the cord around the pulley is mathematically represented as
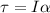
Here
 is the angular acceleration
is the angular acceleration
Here
 is the torque which can be equivalent to
is the torque which can be equivalent to
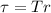
Substituting this above
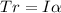
Substituting for T
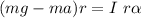
Here
 is the linear acceleration which is mathematically represented as
is the linear acceleration which is mathematically represented as

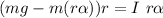

![mgr = \alpha [ I + mr^2]](https://img.qammunity.org/2021/formulas/physics/college/w59to3406gssdg9gd5hsqzycgn6slx3dm7.png)
making
 the subject
the subject
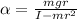
Substituting values
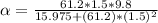
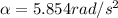
Now substituting into the equation above to obtain the acceleration
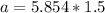
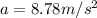
This acceleration is

and v is the linear velocity with is mathematically represented as
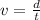
Substituting this into the formula acceleration

making t the subject
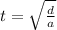
substituting value

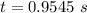
Now the linear velocity is
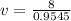
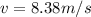
The angular velocity is
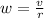
So
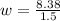
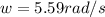
Generally 1 radian is equal to 0.159155 rounds or turns
So 5.59 radian is equal to x
Now x is mathematically obtained as
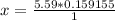
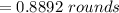
Also
60 second = 1 minute
So 1 second = z
Now z is mathematically obtained as

z
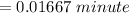
Therefore