Question

There has been a trend toward less driving in the last few years, especially by young people. From 2001 to 2009, the annual vehicle miles traveled by people decreased. Assume the standard deviation was 2000 miles in 2009. Suppose you would like to conduct a survey to develop a 90% confidence interval of the annual vehicle-miles per person for people. A margin of error of 100 miles is desired. How large of a sample should be used for the survey?

Answer 1

The sample size is used for the survey (n) = 1082

Step-by-step explanation:

Step-by-step explanation:-

Step(i):-

Given data There has been a trend toward less driving in the last few years, especially by young people. From 2001 to 2009

Assume the standard deviation was 2000 miles in 2009

Given the Population standard deviation 'σ' = 2000 miles

Given the margin of error at 90% of confidence interval

Margin of error = 100 miles

The z- score value at 90% of confidence interval = 1.645

Step(ii):-

The Margin of error is determined by

`M.E = (Z_(\alpha )S.D )/(√(n) )`

`M.E X √(n) = Z_(\alpha ) S.D`

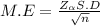
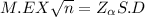
Now the sample size
`√(n) = (Z_(\alpha ) S.D)/(Marginerror) = (1.645 X 2000)/(100)`

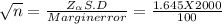
√n = 32.9

squaring on both sides , we get ' n ' = 1082.41

Final answer:-

The sample size is used for the survey (n) = 1082