Question

A researcher is studying a newly discovered gene that causes increased body weight in domesticated chickens. In a mainland population, the frequency of the A1 allele is 0.2, for this gene with two alleles. If 100 of these mainland chicken are transported on a ship to an isolated island with a population of 200 A1A1 chickens, 400 A1A2 chickens, and 400 A2A2 chickens, what would the frequency of the A1 allele in the admixed population

Answer 1

0.382

Step-by-step explanation:

In solving this, let's recall the Hardy-Weinberge's equations which are as follows: p + q = 1;
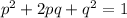`p^(2) + 2pq + q^(2) = 1` , where p represents the dominant Allele, while q represents the recessive allele. In applying this to what we want to calculate,
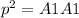`p^(2) = A1A1`, 2pq = A1A2, and
`q^(2) = A2A2`.

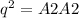Using the Hardy-Weinberge's equations, we can determine the number of individuals having the different types of genotype inherent in the 100 mainland chicken that was transported.

Since p + q = 1, i.e. given that allele frequency of A1 is 0.2, therefore allele frequency for A2 = 0.8 (p + q = 1).

Using
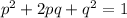`p^(2) + 2pq + q^(2) = 1`, we would have the following:

`p^(2) = A1A1 = 0.2^(2) = 0.04`

`2pq = A1A2 = 2(0.2*0.8) = 0.32`

`qx^(2) = A2A2 = 0.8^(2) = 0.64`

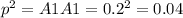
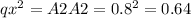
Therefore, number of mainland chickens with the A1A1 genotype = 0.04*100 = 4; A1A2 = 0.32*100 = 32; A2A2 =0.64*100 = 64

The genotype frequencies for the admixed population would be the sum of that of the transported mainland chicken and that of the isolated chicken, which would be:

Genotype mainland isolated Total No of A1 allele present

A1A1 4 200 204 204

A1A2 32 400 432 216

A2A2 64 400 464 0

Total 1100 420

Therefore, allele frequency of the A1 allele in the admixed population = 420/1100 = 0.382