Question

After paying ​$5 to​ play, a single fair die isa single fair die is ​rolled, and you are paid back the number of dollars corresponding to the numberthe number of dots facing up. For​ example, if aa 66 turns​ up, ​$66 is returned to you for a net​ gain, or​ payoff, of​ $1, if aa 44 turns​ up, ​$44 is returned for a net gain of minus−​$1, and so on. What is the expected value of the​ game? Is the game​ fair?

Answer 1

`E(X) = -1.5`

No, the game is not fair since the expected value represents a loss.

Explanation:

The expected value of this game is calculated using

`E(X) = \sum(x_(i)p_(i))`

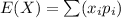
Where
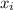`x_(i)` is the net gain of each outcome and
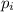`p_(i)` is the probability of each outcome.

When a die is rolled, the probability of getting each outcome is

`p = (1)/(6)`

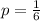
Where 6 is the total number of possible outcomes.

The cost of playing the game is $5

The net gain for each outcome is given by

`x_(1) = 1 - 5 =-4\\x_(2) = 2 - 5 =-3\\x_(3) = 3 - 5 =-2\\x_(4) = 4 - 5 =-1\\x_(5) = 5 - 5 = 0\\x_(6) = 6 - 5 =1\\`

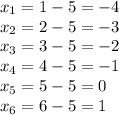
Now we can find the expected value of this game,
`E(X) = (x_(1) \cdot p_(1)) + (x_(2) \cdot p_(2)) +(x_(3) \cdot p_(3))+(x_(4) \cdot p_(4))+(x_(5) \cdot p_(5)) + (x_(6) \cdot p_(6))`

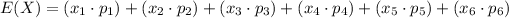
Since the probability of each outcome is same

`E(X) = p(x_(1)+ x_(2)+ x_(3)+ x_(4)+ x_(5)+x_(6)) \\E(X) = (1)/(6) (-4 -3 -2 -1+0+1)\\E(X) = (1)/(6) (-9)\\E(X) = (-9)/(6) \\E(X) = -1.5`

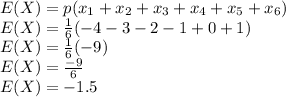
Therefore, we can conclude that this game is not fair since the expected value is negative which represents a loss rather than a gain.