Question

Suppose that a fast food restaurant decides to survey its customers to gauge interest in a breakfast menu. After surveying multiple people, the restaurant created a 95% confidence interval for the proportion of customers interested in a breakfast menu. The confidence interval is (0.688,0.766) . Use the confidence interval to find the point estimate and margin of error for the proportion. Give your answer precise to three decimal places.

Answer 1

`\hat p = 0.727` point of estimate for the proportion of customers interested in a breakfast menu

`ME= 0.039` represent the margin of error.

Explanation:

For this case we want to find a confidence interval for the proportion of customers interested in a breakfast menu.

The confidence interval for this case is given by this formula:

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

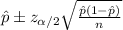
And the margin of error is given by:

`ME = z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

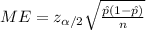
The 95% confidence for this case is given by:

`0.688 \leq p \leq 0.766`

We can find the point of estimate for the proportion using the fact that the interval is symmetrical

`\hat p = (Lower+Upper)/(2) =(0.688+0.766)/(2)=0.727`

And we can find the margin of error with this difference:

`ME = Upper- \hat p = 0.766-0.727 = 0.039`

Or equivalently with:

`ME = \hat p -Lower = 0.727- 0.688 =0.039`

So then the final answer for this case would be:

`\hat p = 0.727` point of estimate for the proportion of customers interested in a breakfast menu

`ME= 0.039` represent the margin of error.