Question

The two right triangular prisms are similar solids.

The scale factor of the larger prism to the smaller prism
is 3. How do the volumes compare?
The volume changes by 3.
The volume changes by
, or 2
The volume changes by
lo

Answer 1

Answer Choice 3

Explanation:

on edge 2020

Answer 2

The volume of the larger prims is eight times greater than the smaller prism.

Explanation:

If the scale factor of the larger prims to the smaller prism is 3, that means each side is triple.

We know the a triangular prims has a volume defined by

`V_(small) =(b * h_(1) )/(2) * h_(2)`

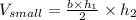
If we take that formula as the smaller prism, then the larer prism has a volum of

`V_(large) =(2b * 2h_(1) )/(2) * 2h_(2)=8((b * h_(1) * h_(2) )/(2) )`

If we compare, we can deduct that

`V_(large)=8V_(small)`

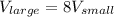
In words, the volume of the larger prims is eight times greater than the smaller prism.