Question

A yearbook company was investigating whether there is a significant difference between two states in the percents of high school students who order yearbooks. From a random sample of 150 students selected from one state, 70 had ordered a yearbook. From a random sample of 100 students selected from the other state, 65 had ordered a yearbook. Which of the following is the most appropriate method for analyzing the results?

A. A one-sample zz-test for a sample proportion
B. A one-sample zz-test for a population proportion
C. A two-sample zz-test for a difference in sample proportions
D. A two-sample zz-test for a difference in population proportions
E. A two-sample zz-test for a population proportion

Answer 1

Null hypothesis:
`p_1 = p_2`

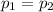
Alternative hypothesis:
`p_1 \\eq p_2`

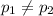
So we need to conduct a:

D. A two-sample z-test for a difference in population proportions

Because the idea is to check if the population proportions in the states are similar or not.

Explanation:

For this case they are trying two proof if there is a significant difference between two states in the percents of high school students who order yearbooks, and we chan check this with the difference of proportions.

Lets say that
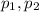`p_1,p_2` are the two proportions of interest and we want to check the following hypothesis:

We have the following info given:

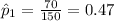`\hat p_1 = (70)/(150)= 0.47` proportion of students that had ordered a yearbook from one state

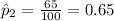`\hat p_2= (65)/(100)= 0.65` proportion of students that had ordered a yearbook from another state

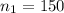`n_1 = 150` sample size from one state

`n_2=100` sample size from another state

Null hypothesis:
`p_1 = p_2`

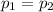
Alternative hypothesis:
`p_1 \\eq p_2`

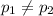
So we need to conduct a:

D. A two-sample z-test for a difference in population proportions

Because the idea is to check if the population proportions in the states are similar or not.