Question

PLEASE ANSWER THIS IS TIMED

What is the equation of the line passing through the points (2, –1) and (5, –10) in slope-intercept form?
y = negative 3 x minus 5
y = negative 3 x + 5
y = 3 x minus 5
y = 3 x + 5

Answer 1

y = -3x + 5

Explanation:

Answer 2

The equation of the line is y = -3x + 5 "i.e. negative 3x + 5"

Explanation:

Given

Points (2,-1) and (5,-10)

Required

Equation of the line

The equation of a line is usually of the form y = mx + b

where m is the gradient or slope of the line and b is the y intercept.

First, the gradient (m) of the line will be calculated;

`Gradient, m = (y_2 - y_1)/(x_2 - x_1)`

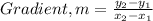
From the given points (2,-1) and (5,-10)

`x_1 = 2; y_1 = -1; x_2 = 5; y_2 = -10`

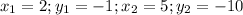
By substituting the right values;

`m = (y_2 - y_1)/(x_2 - x_1)` becomes

`m = (-10 - (-1))/(5 - 2)`

`m = (-10 + 1)/(5 - 2)`

`m = (-9)/(3)`

`m = -3`

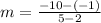
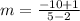
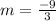
The next step is to calculate the y intercept

Recall that the equation of a line is usually of the form y = mx + b

Substitute
`m = -3` in this equation; we have

y = -3x + b

Make b the subject of formula

b = y + 3x

From the given points (2,-1) and (5,-10)

when x = 2, y = -1

Substitute these values in "b = y + 3x"

b = -1 + 3(2)

b = -1 + 6

b = 5

Also when x = 5, y = -10

Substitute these values in "b = y + 3x"

b = -10 + 3(5)

b = -10+ 15

b = 5

Hence, the y intercept is 5 and the gradient is -3

In other words; b = 5 and m = -3

Substitute these values in y = mx + b

y = -3x + 5

Hence, the equation of the line is y = -3x + 5