Question

patricia is building the community dog park. she plans to build the dog park right beside the city park so she can use one side of the existing fence. her budget allows her yo purchase 340 feet of fencing. in order to make the area of the dog park as large as possible, determine the dimensions of the dog park if one side of the fence is attached to thr city park's fence

Answer 1

85 feet by 170 feet

Explanation:

Let the dimension of the dog park be x and y

Since only three sides will be fenced,

Perimeter, x+2y=340

• x=340-2y

• Area of the Park, A(x,y)=xy

Our goal is to determine the dimension of the park which maximizes the area.

Substituting x=340-2y into A(x,y)

`A(y)=y(340-2y)\\A(y)=-2y^2+340y`

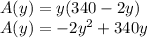
To maximize the area, we find the vertex using the equation of line of symmetry. Note that you can also find the critical points instead.

Equation of symmetry,
`y=-(b)/(2a)`

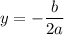
a=-2, b=340

`y=-(340)/(2(-2))=85`

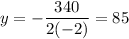
Recall that: x=340-2y

x=340-2(85)=340-170=170 feet

Since x=170 feet, y=85 feet

The dimension of the park which maximizes the area are: 85 feet by 170 feet.

Furthermore, the part opposite the existing fence is 170 feet.